Số chính phương là gì
Định nghĩa: Số chính phương là một số tự nhiên bằng bình phương của một số tự nhiên khác. Nói cách khác, đó là kết quả khi ta nhân một số tự nhiên với chính nó.
Ví dụ:
Các số 4, 9, 16, 25,... là số chính phương vì:
4 = 2 x 2
9 = 3 x 3
16 = 4 x 4
25 = 5 x 5
Hình dung bằng hình học: Nếu bạn vẽ một hình vuông có cạnh bằng số tự nhiên đó, thì diện tích hình vuông sẽ chính là số chính phương tương ứng. Ví dụ, hình vuông có cạnh bằng 3 sẽ có diện tích là 9 (3 x 3).
Tại sao số chính phương lại đặc biệt?
Tính đối xứng: Các số chính phương thường có tính đối xứng đặc biệt khi phân tích ra thừa số nguyên tố. Mỗi thừa số nguyên tố của một số chính phương luôn xuất hiện với số mũ chẵn.
Ứng dụng: Số chính phương có nhiều ứng dụng trong toán học, mật mã học, và cả trong đời sống hàng ngày. Ví dụ, trong thiết kế kiến trúc, người ta thường sử dụng các số chính phương để tạo nên những hình khối cân đối và đẹp mắt.
Tính chất thú vị: Số chính phương còn ẩn chứa nhiều tính chất thú vị khác mà các nhà toán học vẫn đang khám phá. Ví dụ, tổng của hai số chính phương liên tiếp luôn là một số lẻ.
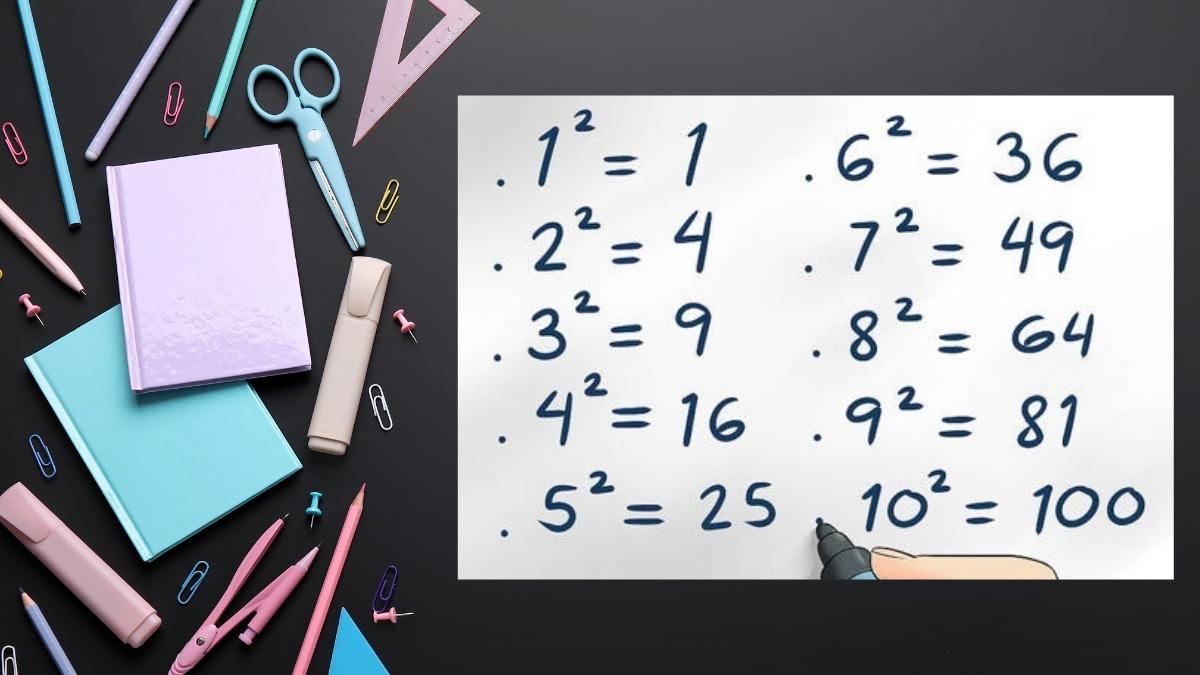
Số chính phương trong toán họcSố chính phương có những tính chất đặc biệt giúp chúng ta phân biệt chúng với các số tự nhiên khác. Dưới đây là một số tính chất quan trọng:
- Chữ số tận cùng: Số chính phương chỉ có thể có các chữ số tận cùng là 0, 1, 4, 5, 6 hoặc 9.
- Phân tích ra thừa số nguyên tố: Khi phân tích một số chính phương ra thừa số nguyên tố, các số mũ của các thừa số nguyên tố đều là số chẵn.
- Tổng các chữ số: Không có quy tắc chung để xác định một số có phải là số chính phương hay không chỉ dựa trên tổng các chữ số của nó. Tuy nhiên, có một số dấu hiệu đặc biệt có thể giúp ta loại trừ một số trường hợp.
- Hình học: Số chính phương biểu diễn diện tích của một hình vuông có cạnh là số tự nhiên.
Tại sao số chính phương lại quan trọng?
Ứng dụng trong toán học: Số chính phương xuất hiện trong nhiều lĩnh vực của toán học, từ số học đến đại số, hình học và cả lý thuyết số.
Ứng dụng trong khoa học tự nhiên: Các số chính phương được sử dụng để mô hình hóa nhiều hiện tượng tự nhiên, như các quy luật về chuyển động, cấu trúc tinh thể, v.v.
Ứng dụng trong mật mã học: Số chính phương đóng vai trò quan trọng trong việc thiết kế các thuật toán mã hóa và giải mã.
Ứng dụng trong kiến trúc và nghệ thuật: Các hình vuông và các hình có liên quan đến số chính phương thường được sử dụng trong thiết kế kiến trúc và các tác phẩm nghệ thuật.
Tham khảo: Đề thi tiếng anh thpt quốc gia 2019 mã 401

Tính chất số chính phươngCâu trả lời ngắn gọn là: Không có số chính phương lớn nhất.
Số chính phương nhỏ nhất: Nếu xét tất cả các số tự nhiên, bao gồm cả số 0, thì số chính phương nhỏ nhất là 0 (vì 0 = 0²). Tuy nhiên, nếu chỉ xét các số tự nhiên dương, thì số chính phương nhỏ nhất là 1 (vì 1 = 1²).
Số chính phương lớn nhất: Không có giới hạn trên cho các số chính phương. Bất kỳ số tự nhiên nào bạn nghĩ ra, luôn có một số chính phương lớn hơn nó. Ví dụ, nếu bạn nghĩ 1000 là số chính phương lớn nhất, tôi có thể đưa ra 1024 = 32² lớn hơn.
Tại sao lại như vậy?
Tính chất của dãy số tự nhiên: Dãy số tự nhiên là vô hạn, nghĩa là luôn có số tự nhiên lớn hơn bất kỳ số nào bạn chọn.
Tính chất của phép nhân: Khi ta nhân hai số tự nhiên lớn, kết quả sẽ càng lớn. Do đó, bằng cách nhân một số tự nhiên lớn với chính nó, ta luôn thu được một số chính phương lớn hơn.
Tham khảo: Nước ion kiềm đóng chai tốt nhất
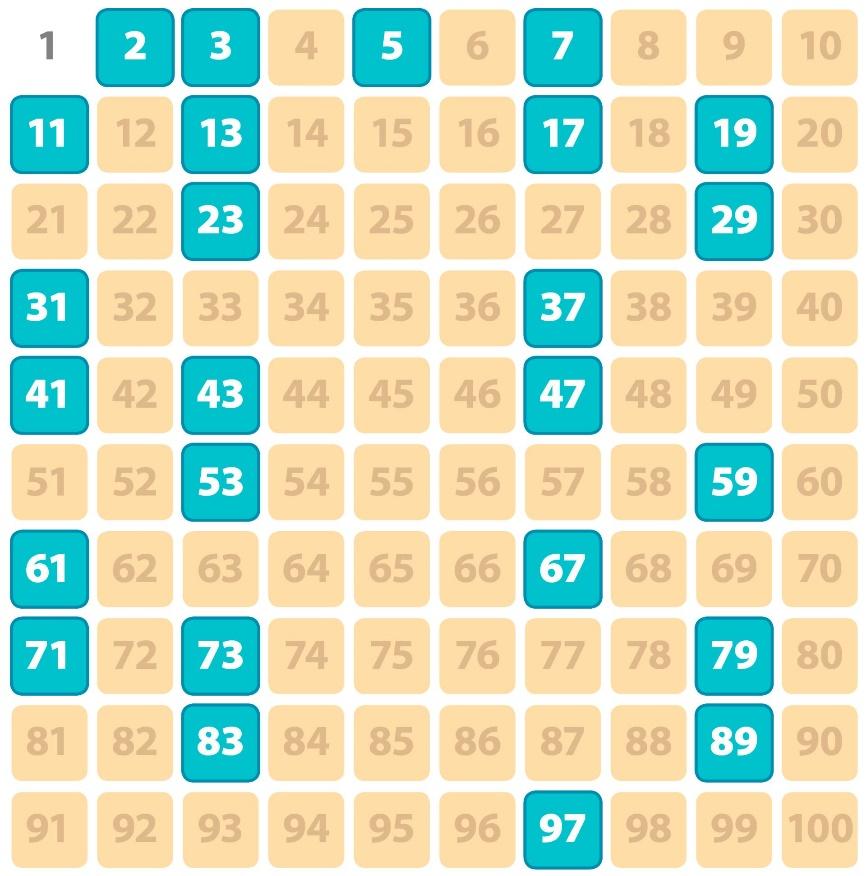
Số chính phươngChữ số tận cùng: Số chính phương chỉ có thể có chữ số tận cùng là 0, 1, 4, 5, 6 hoặc 9. Điều này giúp chúng ta loại bỏ nhanh chóng những số không phải là số chính phương.
Phân tích ra thừa số nguyên tố: Khi phân tích một số chính phương ra thừa số nguyên tố, tất cả các số mũ của các thừa số nguyên tố đều là số chẵn.
Dạng đặc biệt: Số chính phương chỉ có thể có một trong bốn dạng: 4n, 4n + 1, 3n hoặc 3n + 1 (với n là số tự nhiên).
Tính chia hết: Số chính phương chia cho 3 không bao giờ dư 2; chia cho 4 không bao giờ dư 2 hoặc 3. Số chính phương lẻ khi chia cho 8 luôn dư 1.
Số ước số: Số ước nguyên dương của một số chính phương luôn là một số lẻ.
Dạng tổng: Mọi số chính phương đều có thể viết dưới dạng tổng của các số lẻ liên tiếp bắt đầu từ 1.
Các dạng bài tập thường gặp
Chứng minh một số có phải là số chính phương hay không:
- Sử dụng định nghĩa: Kiểm tra xem số đó có thể viết dưới dạng bình phương của một số nguyên hay không.
- Sử dụng tính chất: Áp dụng các tính chất đặc trưng của số chính phương (chữ số tận cùng, tính chia hết...) để loại trừ hoặc khẳng định.
Tìm số chính phương thỏa mãn điều kiện cho trước:
- Đặt ẩn, lập phương trình và giải.
- Sử dụng phương pháp đánh giá.
Bài toán liên quan đến tổng, hiệu, tích của các số chính phương:
- Áp dụng hằng đẳng thức đáng nhớ.
- Sử dụng phương pháp phân tích số.
Trên đây là một số thông tin về chủ đề số chính phương là gì, các tính chất, cách nhận biết số chính phương và một số dạng bài tập về số chính phương. Hi vọng với bài viết trên, các bạn độc giả đã có cho mình thông tin thật hữu ích.
>> Tham khảo: Bảng chữ cái tiếng nhật hiragana