Công thức cấp số cộng
Cấp số cộng là một dãy số mà mỗi số hạng, kể từ số hạng thứ hai, được xác định bằng cách lấy số hạng trước đó cộng với một số không đổi, gọi là công sai.
Nói cách khác, nếu có một dãy số, trong đó hiệu giữa hai số hạng liên tiếp luôn bằng một giá trị cố định, thì dãy số đó được gọi là cấp số cộng. Công sai chính là khoảng cách giữa các số hạng liên tiếp trong dãy.
Ý Nghĩa Của Cấp Số Cộng

Lý thuyết
Ứng Dụng Trong Toán Học: Cấp số cộng là nền tảng quan trọng trong số học và đại số, giúp giải quyết nhiều bài toán về dãy số, tổng dãy số và các bài toán liên quan đến quy luật số học.
Ứng Dụng Trong Thực Tế: Dãy cấp số cộng xuất hiện trong nhiều tình huống thực tế như tính toán lãi suất cố định, quy hoạch tài chính, xây dựng bậc thang, thiết kế kiến trúc và lập kế hoạch sản xuất.
Mô Hình Tăng Trưởng Tuyến Tính: Khi một đại lượng tăng hoặc giảm theo một giá trị cố định theo thời gian, nó có thể được mô tả bằng cấp số cộng, giúp dự đoán xu hướng và đưa ra quyết định hợp lý.
Cấp số cộng không chỉ là một khái niệm toán học mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và đời sống.
Cấp số cộng là một dãy số có quy luật rõ ràng, trong đó mỗi số hạng được tạo ra bằng cách cộng thêm một giá trị cố định, gọi là công sai. Nhờ vào đặc điểm này, cấp số cộng có nhiều tính chất quan trọng giúp đơn giản hóa các phép tính liên quan đến dãy số. Dưới đây là các tính chất cơ bản của cấp số cộng, được trình bày một cách chi tiết hơn.
1. Tính Chất Về Số Hạng Tổng Quát
Mỗi số hạng trong cấp số cộng đều được xác định dựa trên số hạng đầu tiên và công sai. Cụ thể, để tìm một số hạng bất kỳ trong dãy, ta có thể xuất phát từ số hạng đầu tiên rồi liên tiếp cộng thêm công sai nhiều lần. Số lần cộng chính là vị trí của số hạng đó trong dãy trừ đi một. Điều này có nghĩa là nếu biết số hạng đầu tiên và công sai, ta có thể dễ dàng tìm ra bất kỳ số hạng nào trong cấp số cộng mà không cần phải liệt kê toàn bộ dãy số.
2. Tính Chất Ba Số Liên Tiếp
Một đặc điểm quan trọng của cấp số cộng là nếu lấy ba số liên tiếp nhau trong dãy số, thì số hạng đứng ở giữa luôn có giá trị bằng trung bình cộng của hai số hạng đứng trước và sau nó. Điều này xuất phát từ bản chất của công sai – mỗi số hạng trong dãy đều được tạo ra bằng cách cộng thêm một giá trị cố định. Do đó, khoảng cách giữa số hạng đầu tiên và số hạng thứ ba bằng hai lần công sai, còn số hạng giữa nằm chính xác ở vị trí trung bình của hai số hạng này. Tính chất này rất hữu ích trong việc kiểm tra xem ba số có lập thành cấp số cộng hay không mà không cần phải xác định toàn bộ dãy số.
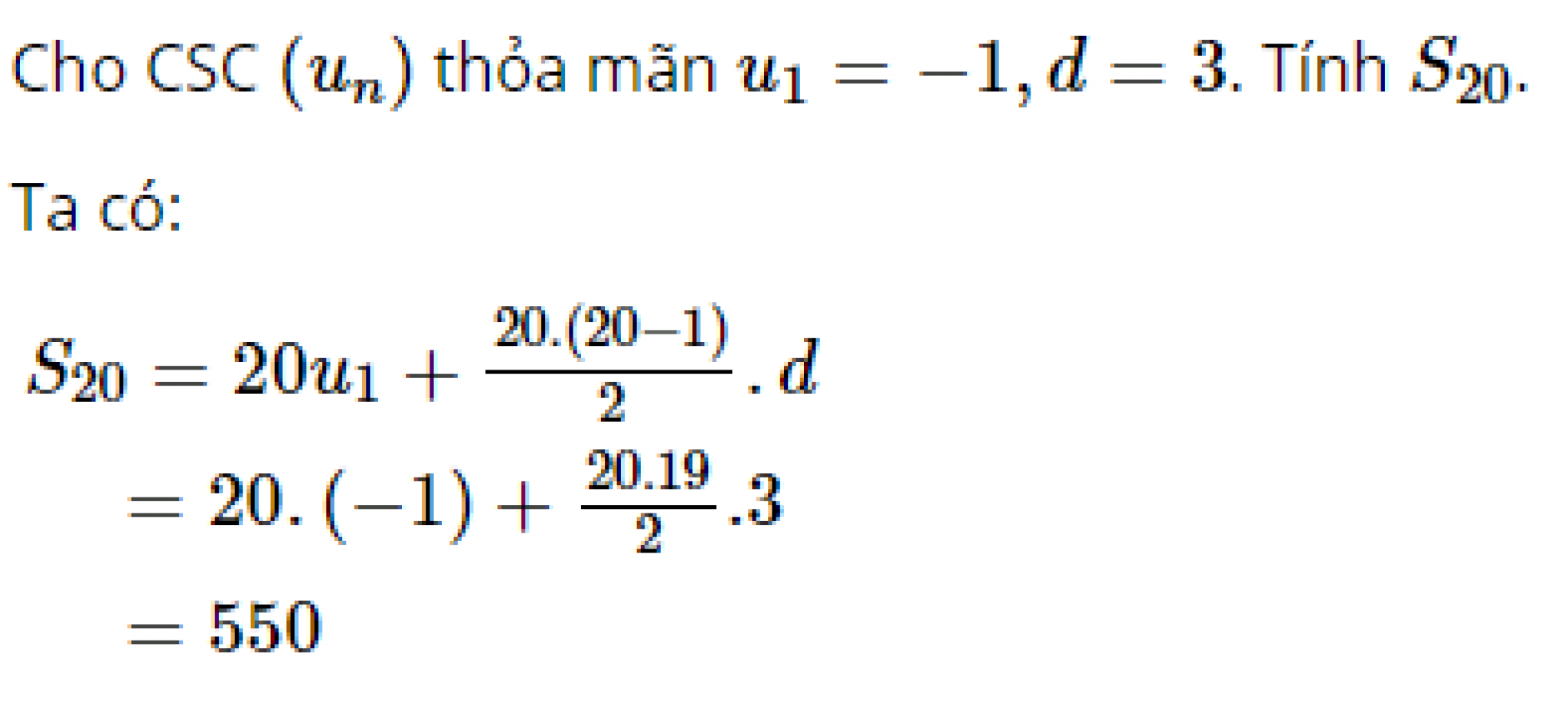
Tính tổng số hạng
3. Tính Chất Về Tổng Các Số Hạng Đầu Tiên
Một tính chất quan trọng khác của cấp số cộng là tổng của một số lượng số hạng đầu tiên có thể tính dễ dàng bằng cách nhân số lượng số hạng với trung bình cộng của số hạng đầu tiên và số hạng cuối cùng trong nhóm số đó. Điều này có nghĩa là nếu biết số hạng đầu tiên, số hạng cuối cùng và số lượng số hạng trong dãy, ta có thể nhanh chóng tính tổng mà không cần phải cộng từng số một. Đây là một tính chất đặc biệt quan trọng khi làm việc với các bài toán tính tổng mà số lượng số hạng rất lớn.
4. Tính Chất Về Công Sai Và Sự Biến Thiên Của Dãy Số
Công sai đóng vai trò quyết định đến xu hướng của một cấp số cộng. Nếu công sai là một số dương, các số hạng trong dãy sẽ liên tục tăng dần, tức là mỗi số hạng lớn hơn số hạng đứng trước nó. Ngược lại, nếu công sai là một số âm, dãy số sẽ giảm dần, nghĩa là mỗi số hạng nhỏ hơn số hạng đứng trước. Nếu công sai bằng không, toàn bộ các số hạng trong dãy sẽ có cùng một giá trị, tức là dãy số không thay đổi mà chỉ bao gồm một số duy nhất được lặp lại nhiều lần.
Nhờ vào tính chất này, có thể dễ dàng xác định xu hướng của một cấp số cộng mà không cần liệt kê tất cả các số hạng. Điều này rất hữu ích trong các bài toán thực tế, chẳng hạn như mô tả sự tăng trưởng của một quỹ tiết kiệm hoặc sự suy giảm của một lượng tài nguyên theo thời gian.
5. Tính Chất Về Trung Bình Cộng Của Các Số Hạng
Một đặc điểm đáng chú ý của cấp số cộng là nếu tính trung bình cộng của tất cả các số hạng trong một nhóm nào đó, thì kết quả thu được sẽ đúng bằng trung bình cộng của số hạng đầu tiên và số hạng cuối cùng trong nhóm đó. Điều này có nghĩa là thay vì phải tính toán từng số riêng lẻ rồi lấy trung bình, ta chỉ cần biết số hạng đầu tiên và số hạng cuối cùng để tìm ra giá trị trung bình.
Tính chất này có ý nghĩa đặc biệt quan trọng khi làm việc với các bài toán đòi hỏi phải tính giá trị trung bình của một tập hợp số liệu có quy luật nhất định, chẳng hạn như tính điểm trung bình của một học sinh theo từng học kỳ hoặc xác định mức lương trung bình của nhân viên trong một công ty có chính sách tăng lương theo năm theo một mức cố định.
Tham khảo: Định lý pytago
Bài 1: Tiết Kiệm Hàng Tháng
Một người gửi tiết kiệm vào ngân hàng, mỗi tháng anh ta gửi thêm một khoản cố định là 500 nghìn đồng. Nếu tháng đầu tiên anh ta gửi 2 triệu đồng, hãy tính số tiền anh ta gửi vào ngân hàng sau 12 tháng.
Bài 2: Bậc Thang Lên Nhà
Một cầu thang có tổng cộng 20 bậc, mỗi bậc có chiều cao tăng đều so với bậc trước đó. Nếu bậc đầu tiên cao 15 cm và mỗi bậc sau cao hơn bậc trước 2 cm, hãy tính chiều cao của bậc cuối cùng.
Bài 3: Thu Nhập Tăng Dần Theo Năm
Một công ty có chính sách tăng lương cố định mỗi năm. Một nhân viên có mức lương khởi điểm là 8 triệu đồng/tháng và công ty tăng lương 500 nghìn đồng mỗi năm. Hỏi sau 6 năm, mức lương của nhân viên đó là bao nhiêu?
Bài 4: Đường Chạy Trong Sân Vận Động
Một vận động viên tập chạy trên sân, ngày đầu tiên anh ta chạy 2 km và mỗi ngày sau đó anh ta tăng thêm 500 mét so với ngày trước. Hỏi sau 10 ngày, tổng quãng đường mà anh ta đã chạy là bao nhiêu km?
Bài 5: Ghế Ngồi Trong Khán Đài
Một rạp hát có các hàng ghế được sắp xếp theo cấp số cộng. Hàng đầu tiên có 15 ghế, mỗi hàng tiếp theo có thêm 2 ghế so với hàng trước. Nếu rạp có tổng cộng 20 hàng, hãy tính số ghế ở hàng cuối cùng.
Bài 6: Mua Sách Hằng Tháng
Một học sinh có kế hoạch mua sách để học, tháng đầu tiên mua 3 cuốn, sau đó mỗi tháng mua thêm 2 cuốn so với tháng trước. Hỏi sau 8 tháng, tổng số sách mà học sinh đó đã mua là bao nhiêu cuốn?
Bài 7: Xây Dựng Dãy Nhà
Một khu phố có một dãy nhà được xây theo quy luật, nhà đầu tiên có diện tích 40 mét vuông, mỗi căn tiếp theo có diện tích lớn hơn căn trước 5 mét vuông. Nếu có 12 căn nhà trong dãy, hãy tính diện tích của căn nhà cuối cùng.
Bài 8: Trồng Cây Theo Hàng
Một người nông dân trồng cây theo hàng, hàng đầu tiên có 10 cây, mỗi hàng tiếp theo có nhiều hơn hàng trước 3 cây. Nếu có tổng cộng 15 hàng cây, hãy tính tổng số cây đã được trồng.
Những bài tập trên áp dụng công thức của cấp số cộng để giải quyết các vấn đề thực tế trong cuộc sống, giúp hiểu rõ hơn về quy luật tăng dần và cách tính toán nhanh chóng.
Công thức