Số chính phương là gì?
Trong toán học, số chính phương (hay còn gọi là số bình phương hoàn chỉnh) là một số nguyên dương có thể biểu diễn dưới dạng bình phương của một số nguyên khác.
Hiểu đơn giản: Một số nguyên a là số chính phương nếu tồn tại một số nguyên b sao cho a = b².
Ví dụ:
1 = 1²
4 = 2²
9 = 3²
16 = 4²
25 = 5²
⇒ Các số 1, 4, 9, 16, 25,... là những số chính phương.
Lưu ý:
Số 0 cũng được coi là số chính phương vì 0 = 0².
Số âm không thể là số chính phương vì bình phương của mọi số nguyên đều không âm.
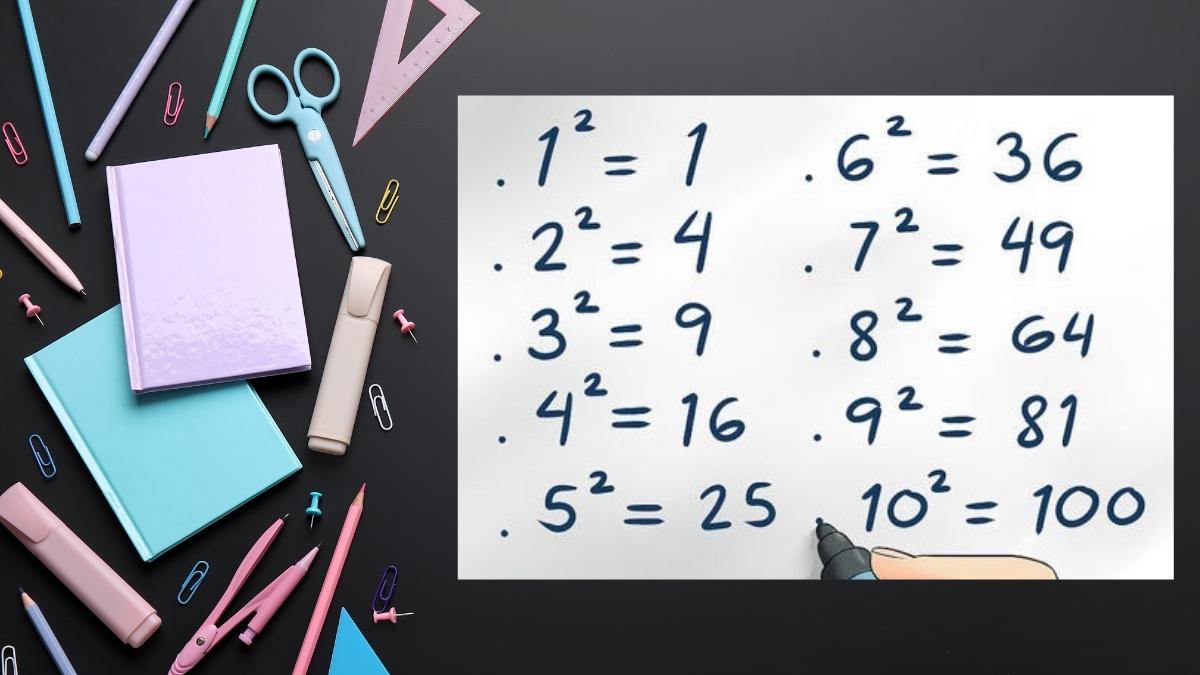
Số chính phương trong toán họcSố chính phương có nhiều tính chất đặc biệt giúp chúng ta nhận biết và phân biệt chúng với các số khác.
Kết thúc bằng các chữ số đặc biệt
Các số chính phương chỉ có thể kết thúc bằng: 0, 1, 4, 5, 6, hoặc 9.
Không có số chính phương nào kết thúc bằng 2, 3, 7 hoặc 8.
Ví dụ:
36 → kết thúc bằng 6 → có thể là số chính phương
49 → kết thúc bằng 9 → là số chính phương (vì 7² = 49)
78 → kết thúc bằng 8 → chắc chắn không phải số chính phương
Số chính phương có căn bậc hai là số nguyên
Một đặc điểm rõ ràng nhất để nhận biết số chính phương là: Lấy căn bậc hai của nó phải ra số nguyên.
Ví dụ:
√81 = 9 → 81 là số chính phương
√50 ≈ 7.07 → không phải số nguyên → 50 không phải số chính phương
Số chính phương có số lượng ước lẻ
Các số chính phương luôn có số lượng ước là số lẻ, vì có một ước số lặp lại (chính căn bậc hai).
Ví dụ:
36 có các ước: 1, 2, 3, 4, 6, 9, 12, 18, 36 → tổng cộng 9 ước
36 là số chính phương vì có số ước lẻ
Một số chính phương chia hết cho một số nguyên thì cũng chia hết cho bình phương của số đó
Ví dụ:
36 chia hết cho 6 → cũng chia hết cho 6² = 36
81 chia hết cho 3 → cũng chia hết cho 3² = 9
Một số chính phương luôn là tổng của các số lẻ liên tiếp
Công thức:
1 + 3 + 5 + 7 + ... + (2n - 1) = n²
Ví dụ:
1 + 3 = 4 → 2²
1 + 3 + 5 = 9 → 3²
1 + 3 + 5 + 7 + 9 = 25 → 5²
Các số chính phươngSố chính phương tuy đơn giản nhưng có nhiều ứng dụng thực tiễn.
Trong học tập và toán học
Dùng để giải phương trình bậc hai: nếu vế phải là số chính phương thì dễ tìm nghiệm hơn
Trong các bài toán hình học về diện tích hình vuông
Ứng dụng trong các định lý như định lý Pytago
Sử dụng trong phân tích đa thức, hằng đẳng thức đáng nhớ
Ví dụ: a² + 2ab + b² = (a + b)² → đây là biểu thức có số chính phương
Trong lập trình và thuật toán
Kiểm tra số chính phương là gì bước quan trọng trong việc tối ưu hóa chương trình, đặc biệt là các bài toán số học
Dùng trong mã hóa, xử lý số, kiểm tra độ hoàn hảo của thuật toán
Trong xây dựng và thiết kế
Dễ tính toán diện tích nếu các cạnh là số chính phương là gì
Dùng để thiết kế hình vuông hoặc các hình vuông con trong kiến trúc, nội thất
Trong đời sống hàng ngày
Dễ dàng đo đạc, chia nhỏ các vùng có diện tích vuông
Ghi nhớ đơn giản hơn khi xử lý các số có dạng bình phương như 100, 400, 900...

Học sinh trong giờ ToánLàm sao để kiểm tra một số có phải là số chính phương?
Cách đơn giản nhất là lấy căn bậc hai của số đó.
Nếu căn bậc hai là số nguyên → là số chính phương.
Nếu không → không phải.
Ví dụ:
√121 = 11 → 121 là số chính phương
√50 ≈ 7.07 → không nguyên → 50 không phải
Có bao nhiêu số chính phương nhỏ hơn 1000?
Ta tìm số lớn nhất mà bình phương vẫn ≤ 1000.
Ta có: 31² = 961 < 1000
⇒ Có 31 số chính phương nhỏ hơn 1000 (từ 1² đến 31²)
Số 0 có phải là số chính phương không?
Có. Vì 0 = 0².
Số 0 vẫn là bình phương của một số nguyên nên vẫn được xem là số chính phương.
Số âm có phải là số chính phương không?
Không. Vì bình phương của mọi số nguyên luôn không âm, nên không có số chính phương âm.
Ví dụ:
-5 × -5 = 25 → không thể nào có -25 là số chính phương
Số chính phương có thể là số nguyên tố không?
Không. Vì nếu một số là số chính phương thì nó có ít nhất 3 ước số (1, chính nó, và căn bậc hai).
Trong khi số nguyên tố chỉ có đúng 2 ước là 1 và chính nó.
Ví dụ:
4 là số chính phương → có các ước: 1, 2, 4
4 không phải số nguyên tố
Có số nào vừa là số chính phương vừa là số hoàn hảo không?
Có. Ví dụ:
Số 36 là số chính phương (6²)
36 có tổng các ước đúng bằng 36 → là số hoàn hảo
Tuy nhiên, các số vừa là số chính phương vừa hoàn hảo là rất hiếm.
Có quy luật nào giúp ghi nhớ nhanh các số chính phương không?
Có thể học thuộc bảng bình phương từ 1 đến 30, rất phổ biến trong học toán:
1² = 1
2² = 4
3² = 9
4² = 16
5² = 25
6² = 36
7² = 49
8² = 64
9² = 81
10² = 100
... đến
30² = 900
Số chính phương là gì một khái niệm nền tảng trong toán học, xuất hiện nhiều trong các bài toán, công thức và ứng dụng thực tế. Việc nắm chắc định nghĩa, đặc điểm nhận biết cũng như hiểu rõ ứng dụng của số chính phương không chỉ giúp bạn học tốt môn Toán mà còn phát triển tư duy logic, giải quyết vấn đề hiệu quả hơn trong nhiều lĩnh vực.
Khi luyện tập và làm bài, hãy ghi nhớ một số mẹo nhận biết nhanh số chính phương và luyện tập với bảng bình phương từ 1 đến 30 để tăng khả năng nhận diện nhanh chóng. Đặc biệt, đừng quên rằng số chính phương chỉ có căn bậc hai là số nguyên, và luôn kết thúc bằng các chữ số 0, 1, 4, 5, 6 hoặc 9.