Công thức cấp số cộng
Cấp số cộng là một dãy số trong đó mỗi số hạng (từ số thứ hai trở đi) đều bằng số hạng đứng trước cộng với một số không đổi, gọi là công sai (ký hiệu là d).
Ký hiệu tổng quát một cấp số cộng: a, a+d, a+2d, a+3d, …
Trong đó:
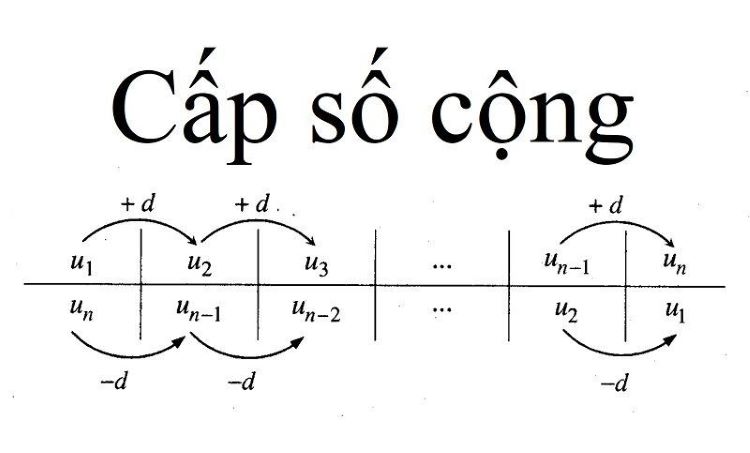
Giải thích
a là số hạng đầu tiên,
d là công sai, 𝑎𝑛=a+(n− 1)d là số hạng tổng quát thứ n.
Ví dụ: Dãy 3, 5, 7, 9, 11 là cấp số cộng với công sai 𝑑=2
Trong toán học, để sử dụng chính xác công thức của cấp số cộng, người học cần hiểu rõ các yếu tố cấu thành nên dãy cấp số cộng. Những yếu tố này không chỉ giúp xác định được bản chất của dãy mà còn là cơ sở để xây dựng các công thức tính toán và giải bài tập thực tế.
a. Số hạng đầu tiên (ký hiệu thường dùng là a):
Đây là số hạng đầu tiên xuất hiện trong dãy cấp số cộng. Nó đóng vai trò làm mốc khởi đầu để xây dựng nên các số hạng tiếp theo. Khi biết số hạng đầu tiên, ta có thể xác định toàn bộ dãy nếu biết thêm công sai và số lượng số hạng.
b. Công sai (ký hiệu là d):
Công sai là hiệu số giữa hai số hạng liên tiếp bất kỳ trong dãy, và đặc biệt là không đổi trong toàn bộ dãy. Nghĩa là, mỗi số hạng sau đều được tạo thành bằng cách cộng thêm công sai vào số hạng đứng trước đó. Công sai dương tạo ra dãy tăng đều, công sai âm tạo ra dãy giảm đều, còn công sai bằng 0 thì dãy là dãy hằng (các số hạng bằng nhau).

Lý thuyết
c. Số hạng tổng quát (ký hiệu thường là 𝑢𝑛):
Đây là biểu thức giúp xác định giá trị của số hạng thứ n bất kỳ trong dãy mà không cần phải liệt kê các số hạng đứng trước nó. Số hạng tổng quát là sự kết hợp của số hạng đầu tiên, công sai và vị trí của số hạng cần tìm. Nó là công cụ quan trọng trong các bài toán tìm số hạng ở vị trí xa mà không cần viết ra toàn bộ dãy.
d. Tổng các số hạng đầu (ký hiệu thường là 𝑆𝑛)
Tổng này biểu thị tổng giá trị của một số lượng nhất định các số hạng liên tiếp kể từ đầu dãy. Trong bài toán thực tế, tổng này rất hay được dùng trong các bài toán cộng dồn, lập kế hoạch, tính khoảng cách, chi phí hoặc tổng hợp dữ liệu. Biểu thức tính tổng phụ thuộc vào số hạng đầu, số lượng số hạng, và công sai.
Tóm lại, các yếu tố trên tạo thành nền tảng của dãy cấp số cộng. Chỉ khi nắm vững từng yếu tố, người học mới có thể áp dụng hiệu quả công thức của cấp số cộng trong việc giải các bài toán từ cơ bản đến nâng cao, cũng như ứng dụng vào các tình huống thực tế như tài chính, lập lịch, hay kỹ thuật.
1. Suy luận công thức số hạng tổng quát của cấp số cộng
Giả sử ta có một cấp số cộng gồm các số hạng liên tiếp. Gọi số hạng đầu tiên là một giá trị khởi đầu, và hiệu giữa hai số hạng liên tiếp là một giá trị không đổi (còn gọi là công sai).
Khi đó, số hạng thứ hai bằng số hạng đầu tiên cộng với công sai.
Số hạng thứ ba sẽ bằng số hạng đầu tiên cộng hai lần công sai.
Tiếp tục theo quy luật đó, số hạng thứ n sẽ bằng số hạng đầu tiên cộng với công sai nhân với số lần lặp lại của khoảng cách giữa các số, tức là một số nhỏ hơn n đơn vị.
Do đó, ta suy ra được:
Số hạng tổng quát trong cấp số cộng được tính bằng:
→ số hạng đầu tiên cộng với tích của công sai và hiệu giữa số thứ tự và đơn vị thứ nhất.
2. Suy luận công thức tính tổng n số hạng đầu tiên
Giả sử ta có n số hạng đầu tiên của một cấp số cộng. Số hạng đầu là một giá trị nhất định, và số hạng cuối cùng cũng có thể được biểu diễn dựa vào số hạng đầu và công sai.
Ta xét tổng của dãy theo hai cách:

Công thức
Cách một: viết dãy từ đầu đến cuối.
Cách hai: viết ngược lại từ số hạng cuối về đầu.
Khi cộng hai dãy này lại theo từng cặp số hạng cùng vị trí (một từ đầu, một từ cuối), ta thấy rằng mỗi cặp cộng lại sẽ cho ra cùng một kết quả, vì công sai là đều nhau.
Số lượng cặp bằng tổng số hạng chia đôi, và mỗi cặp đều bằng tổng của số hạng đầu và cuối.
Từ đó, ta suy ra tổng của n số hạng đầu tiên bằng:
→ số lượng số hạng nhân với trung bình cộng của số hạng đầu và số hạng cuối.
3. Lưu ý trong quá trình chứng minh
Chứng minh dựa hoàn toàn vào định nghĩa và tính chất không đổi của công sai.
Cần phân biệt rõ giữa số thứ tự của số hạng và giá trị của số hạng đó.
Việc hoán đổi vị trí dãy để suy luận tổng là một cách tư duy rất đặc trưng trong cấp số cộng, giúp dễ hiểu hơn trong lập luận toán học.
1. Nhầm lẫn giữa công thức số hạng và công thức tổng:
Một lỗi phổ biến là sử dụng sai công thức khi giải bài tập. Nhiều học sinh nhầm công thức tính số hạng tổng quát với công thức tính tổng các số hạng. Điều này thường xảy ra khi không phân biệt rõ mục đích của từng công thức trong từng dạng bài cụ thể.
2. Nhầm thứ tự các yếu tố trong công thức:
Học sinh đôi khi đảo lộn vị trí của các biến, đặc biệt là vị trí của số hạng đầu và công sai. Việc viết sai thứ tự hoặc áp dụng sai vị trí sẽ dẫn đến kết quả sai, dù có thay đúng các giá trị đã biết.
3. Áp dụng công thức cấp số cộng cho dãy không phải cấp số cộng:
Đây là lỗi nghiêm trọng khi người học chưa xác định chính xác dãy số có phải là cấp số cộng hay không. Việc vội vàng áp dụng công thức cho một dãy không tuân theo định nghĩa sẽ làm sai toàn bộ bài toán.
4. Không kiểm tra điều kiện áp dụng:
Một số công thức cấp số cộng chỉ áp dụng khi dãy đã xác định đủ các yếu tố như số hạng đầu, công sai và vị trí các số hạng. Thiếu kiểm tra điều kiện khiến học sinh tính toán theo giả định sai lệch.
5. Bỏ sót hoặc nhầm lẫn các chỉ số trong biểu thức:
Các biểu thức trong cấp số cộng có thể dùng chỉ số biểu diễn vị trí số hạng. Nếu bỏ quên hoặc viết sai chỉ số, bài giải sẽ mất logic và dẫn đến sai lệch kết quả.
6. Không xác định đúng mục tiêu bài toán:
Nhiều bài toán yêu cầu tìm công sai, tổng, hoặc số hạng cụ thể. Nếu học sinh không xác định rõ điều này từ đầu, dễ dẫn đến việc sử dụng công thức không phù hợp với yêu cầu bài.
7. Thiếu bước chứng minh hoặc giải thích logic khi cần:
Trong các bài toán chứng minh hoặc suy luận, học sinh thường chỉ thay công thức mà không giải thích lý do hay mối liên hệ giữa các yếu tố, làm mất tính chặt chẽ của lời giải.