Công thức cấp số cộng
Cấp số cộng là gì?
Cấp số cộng (CSC) là một dãy số mà trong đó hiệu của hai số hạng liên tiếp luôn bằng một hằng số. Hằng số này được gọi là công sai, ký hiệu là d.
Nếu a₁ là số hạng đầu tiên, thì dãy số a₁, a₂, a₃, … là cấp số cộng khi:
a₂ - a₁=a₃ - a₂=… =d
Đặc điểm của cấp số cộng:
Hiệu giữa các số hạng liên tiếp bằng công sai (d):
aₙ₊₁ - aₙ=d với mọi n ≥ 1
Số hạng tổng quát: aₙ=a₁+(n - 1)d
Tổng n số hạng đầu tiên: Sₙ=n/2 × (a₁ + aₙ)=n/2 × [2a₁+(n - 1)d]
Tăng/giảm đều:
Nếu d > 0 → dãy số tăng dần
Nếu d < 0 → dãy số giảm dần
Ứng dụng:
Cấp số cộng xuất hiện trong các bài toán thực tế như: tính lãi, lập kế hoạch, phân bố đều, hoặc các dãy số theo quy luật tuyến tính.

Cấp số cộng là gì và có những đặc điểm nàoCông thức tính số hạng tổng quát trong cấp số cộng
Trong cấp số cộng, số hạng tổng quát aₙ được tính dựa trên số hạng đầu tiên a₁ và công sai d.
Công thức:
aₙ=a₁+(n - 1) × d
Trong đó:
aₙ: số hạng thứ n
a₁: số hạng đầu tiên
d: công sai (hiệu giữa hai số hạng liên tiếp)
n: vị trí số hạng cần tìm
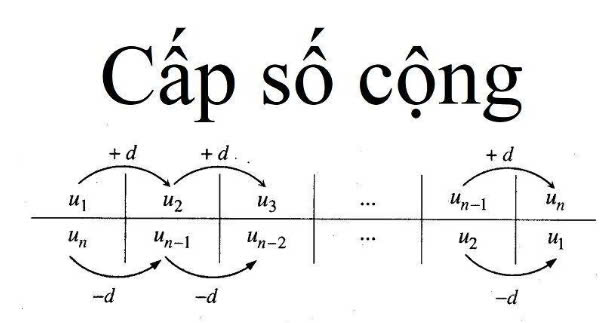
Công thức tính số hạng tổng quát trong cấp số cộngCấp số cộng không phụ thuộc vào dấu của các số hạng, nên công thức tính số hạng tổng quát và công thức tổng n số hạng đầu tiên vẫn áp dụng với dãy số âm.
Công thức số hạng tổng quát:
aₙ=a₁+(n - 1) × d
Công thức tổng n số hạng đầu tiên:
Sₙ=n/2 × (a₁ + aₙ)=n/2 × [2a₁+(n - 1)d]
Ví dụ minh họa với dãy âm:
Dãy số: -2, -5, -8, …
a₁=-2, d=-3
Số hạng thứ 4: a₄=-2+(4 - 1) × (-3)=-2+(-9)=-11
Tổng 4 số hạng đầu: S₄=4/2 × (-2 + -11)=2 × (-13)=-26
Như vậy, công thức cấp số cộng hoàn toàn áp dụng cho dãy số âm.

Công thức tổng quát của cấp số cộngBài toán:
Cho dãy số: 3, 7, 11, …
a₁=3
a₂=7
Tìm số hạng thứ 10 và tổng 10 số hạng đầu tiên.
Bước 1: Tìm công sai (d)
Công sai d=a₂ - a₁=7 - 3=4
Bước 2: Tìm số hạng thứ 10 (a₁₀)
Sử dụng công thức số hạng tổng quát:
aₙ=a₁+(n - 1) × d
a₁₀=3+(10 - 1) × 4=3+36=39
Bước 3: Tính tổng 10 số hạng đầu tiên (S₁₀)
Sử dụng công thức tổng n số hạng đầu tiên:
Sₙ=n/2 × (a₁ + aₙ)
S₁₀=10/2 × (3 + 39)=5 × 42=210
Kết luận:
Số hạng thứ 10: 39
Tổng 10 số hạng đầu: 210
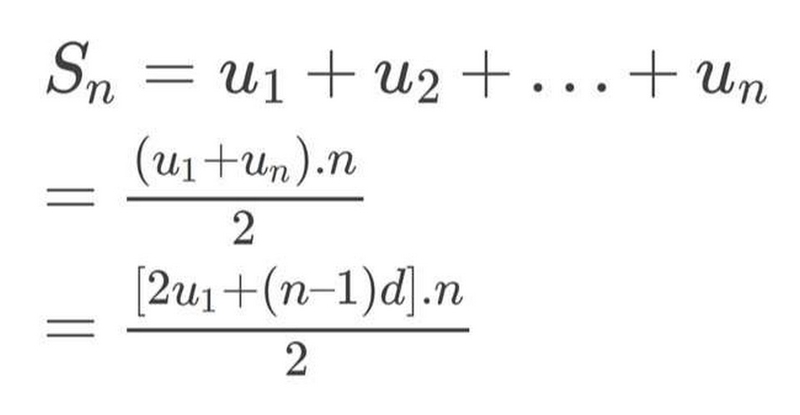
Các bài toán nâng cao về cấp số cộng thường gặpBài toán 1: Tìm số hạng thứ n khi biết tổng n số hạng đầu
Đề bài:
Tổng 5 số hạng đầu tiên của một cấp số cộng là 40. Số hạng đầu tiên là 4. Tìm số hạng thứ 5.
Lời giải:
Công thức tổng n số hạng đầu:
Sₙ=n/2 × (a₁ + aₙ)
Thay các giá trị:
40=5/2 × (4 + a₅)
40 × 2 / 5=4+a₅
16=4+a₅
a₅=12
Kết luận: Số hạng thứ 5 là 12.
Bài toán 2: Tìm số hạng đầu hoặc công sai khi biết tổng một dãy
Đề bài:
Tổng 8 số hạng đầu của một cấp số cộng là 64. Số hạng thứ 8 là 16. Tìm số hạng đầu.
Lời giải:
Công thức tổng n số hạng đầu:
S₈=8/2 × (a₁ + a₈)=4 × (a₁ + 16)=64
a₁+16=16
a₁=0
Kết luận: Số hạng đầu là 0.
Bài toán 3: Tìm công sai khi biết một số hạng và tổng
Đề bài:
Một cấp số cộng có số hạng đầu 3. Tổng 6 số hạng đầu là 48. Tìm công sai d.
Lời giải:
S₆=6/2 × (2a₁ + (6 - 1)d)
48=3 × (2× 3 + 5d)
48=3 × (6 + 5d)
48=18+15d
15d=30
d=2
Kết luận: Công sai là 2.
Bài toán 4: Bài toán thực tế – lương tăng đều theo tháng
Đề bài:
Một nhân viên có lương tháng đầu là 5 triệu. Mỗi tháng tăng thêm 500 nghìn. Hỏi sau 12 tháng tổng lương nhận được là bao nhiêu?
Lời giải:
Đây là cấp số cộng: a₁=5, d=0.5 (triệu), n=12
Tổng 12 số hạng đầu:
S₁₂=12/2 × [2× 5+(12-1)× 0.5]
S₁₂=6 × [10+5.5]=6 × 15.5=93 (triệu)
Kết luận: Tổng lương 12 tháng là 93 triệu.
Cấp số cộng là một dãy số mà hiệu giữa các số hạng liên tiếp luôn bằng một hằng số, gọi là công sai. Hai công thức quan trọng trong cấp số cộng là công thức tính số hạng tổng quát và công thức tính tổng n số hạng đầu tiên.
Số hạng tổng quát được tính bằng:
aₙ=a₁+(n - 1) × d
Tổng n số hạng đầu tiên được tính bằng:
Sₙ=n/2 × (a₁ + aₙ)=n/2 × [2a₁+(n - 1)d]
Trong thực tế, công thức tổng quát của cấp số cộng được áp dụng rất rộng rãi. Chẳng hạn, khi tính lương hoặc thu nhập tăng đều theo tháng, nếu nhân viên có lương tháng đầu là 5 triệu và mỗi tháng tăng thêm 500 nghìn, tổng lương sau 12 tháng có thể tính nhanh bằng công thức tổng n số hạng đầu. Việc này giúp tiết kiệm thời gian và giảm sai sót so với tính từng tháng.
Cấp số cộng còn hữu ích trong việc phân bổ đều chi phí hoặc tài nguyên. Khi cần tăng dần ngân sách, sản lượng hoặc số lượng sản phẩm theo từng giai đoạn, áp dụng công thức tổng quát giúp xác định tổng chi phí hoặc tổng sản phẩm một cách chính xác và nhanh chóng.
Trong quản lý tài chính cá nhân, nếu bạn tiết kiệm mỗi tháng nhiều hơn tháng trước một số tiền cố định, tổng tiền tiết kiệm sau n tháng cũng được tính bằng tổng n số hạng đầu của cấp số cộng. Điều này giúp lập kế hoạch tiết kiệm khoa học và dự đoán chính xác số tiền tích lũy theo thời gian.
Cấp số cộng cũng được sử dụng trong lập lịch trình hoặc kế hoạch tuyến tính. Ví dụ, khi lên kế hoạch tăng dần số lượng công việc, sản phẩm, hoặc thời gian dành cho mỗi nhiệm vụ, áp dụng cấp số cộng giúp phân bổ đều và dễ theo dõi tiến độ.
Như vậy, công thức tổng quát của cấp số cộng không chỉ là kiến thức toán học mà còn là công cụ hữu ích trong thực tiễn, hỗ trợ tính toán, lập kế hoạch và quản lý tài nguyên một cách hiệu quả.
Trên đây chúng tôi đã giới thiệu chi tiết về công thức cấp số cộng, bao gồm số hạng tổng quát, tổng n số hạng đầu tiên, cùng các ví dụ minh họa và ứng dụng thực tế. Hy vọng qua bài viết công thức cấp số cộng này, bạn đọc có thể nắm vững kiến thức, vận dụng linh hoạt trong học tập và các tình huống thực tế.